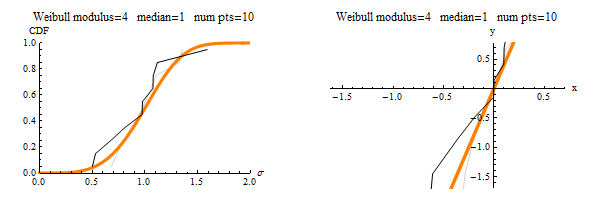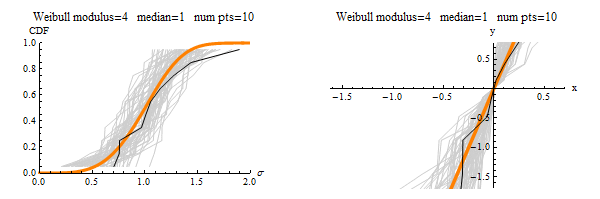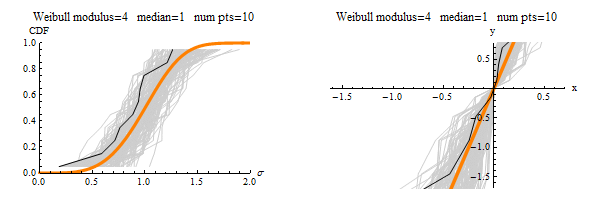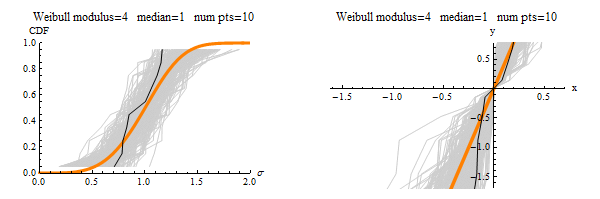This animation shows three ways to visualize a rotation:
The free share link (available until May 24, 2018) is…https://authors.elsevier.com/a/1WqS83PCJl7pmB.
Abstract: Even if a ceramic’s homogenized properties (such as anisotropically evolving stiffness) truly can be predicted from complete knowledge of sub-continuum morphology (e.g., locations, sizes, shapes, orientations, and roughness of trillions of crystals, dislocations, impurities, pores, inclusions, and/or cracks), the necessary calculations are untenably hypervariate. Non-productive (almost derailing) debates over shortcomings of various first-principles ceramics theories are avoided in this work by discussing numerical coarsening in the context of a pedagogically appealing buckling foundation model that requires only sophomore-level understanding of springs, buckling hinges, dashpots, etc. Bypassing pre-requisites in constitutive modeling, this work aims to help students to understand the difference between damage and plasticity while also gaining experience in Monte-Carlo numerical optimization via scale-bridging that reduces memory and processor burden by orders of magnitude while accurately preserving aleatory (finite-finite-sampling) perturbations that are crucial to accurately predict bifurcations, such as ceramic fragmentation.
This publication helps to set knowledge needed to migrate cracks from initially uniform orientations (represented as dots on the left sphere) to highly textured orientations of vertical cracking (or any other texture based on the loading history).
This publication uses this simple system to explain many complicated concepts:
This paper would serve as a good project for a smart undergrad or first-year grad student to reproduce the results. It would serve as a familiarization exercise to learn basics of scale bridging, the difference between damage and plasticity, the influence of loading rate, the influence of microscale perturbations in macroscale behavior (e.g. reducing peak strength and scale effects), and binning down an excessively large number of internal variables to obtain a tractable decimated set. All of that without needing to know anything about constitutive modeling – just a basic knowledge of springs and rigid links would be needed.
Again: see it for free (until May 24) at
https://authors.elsevier.com/a/1WqS83PCJl7pmB
Python source code is available on request.
Cite the paper as:
Brannon, R., Jensen, K., and Nayak, D., Journal of the European Ceramic Society (2018), https://doi.org/10.1016/j.jeurceramsoc.2018.02.036
Sophomore undergraduate, Katharin Jensen, has developed an easily understood illustration of the effect of aleatory uncertainty, which means natural point-to-point variability in systems. She has put statistical variability on the lengths of buckling elements in the following system:
M.Y. Lee, R.M. Brannon and D.R. Bronowski
Explosive failure of the SICN-UC02 specimen (12.7 mm in diameter and 25.4 mm in length) subjected to the unconfined uniaxial compressive stress condition
To establish mechanical properties and failure criteria of silicon carbide (SiC-N) ceramics, a series of quasi-static compression tests has been completed using a high-pressure vessel and a unique sample alignment jig. This report summarizes the test methods, set-up, relevant observations, and results from the constitutive experimental efforts. Combining these quasistatic triaxial compression strength measurements with existing data at higher pressures naturally results in different values for the least-squares fit to this function, appropriate over a broader pressure range. These triaxial compression tests are significant because they constitute the first successful measurements of SiC-N compressive strength under quasistatic conditions. Having an unconfined compressive strength of ~3800 MPa, SiC-N has been heretofore tested only under dynamic conditions to achieve a sufficiently large load to induce failure. Obtaining reliable quasi-static strength measurements has required design of a special alignment jig and loadspreader assembly, as well as redundant gages to ensure alignment. When considered in combination with existing dynamic strength measurements, these data significantly advance the characterization of pressure-dependence of strength, which is important for penetration simulations where failed regions are often at lower pressures than intact regions.
Available Online:
http://www.mech.utah.edu/~brannon/pubs/2004LeeBrannonBronowskiTriaxTestsSiC.pdf
http://www.osti.gov/bridge/purl.cover.jsp?purl=/920770-6YyIPp/
H.W. Meyer Jr. and R.M. Brannon
[This post refers to the original on-line version of the publication. The final (paper) version with page numbers and volume is found at http://dx.doi.org/10.1016/j.ijimpeng.2010.09.007. Some further details and clarifications are in the 2012 posting about this article]
Simulation results for a reference volume of 0.000512 cm^3 ; sf is the size effect factor
Continuum mechanics codes modeling failure of materials historically have considered those materials to be homogeneous, with all elements of a material in the computation having the same failure properties. This is, of course, unrealistic but expedient. But as computer hardware and software has evolved, the time has come to investigate a higher level of complexity in the modeling of failure. The Johnsone-Cook fracture model is widely used in such codes, so it was chosen as the basis for the current work. The CTH finite difference code is widely used to model ballistic impact and penetration, so it also was chosen for the current work. The model proposed here does not consider individual flaws in a material, but rather varies a material’s Johnsone-Cook parameters from element to element to achieve in homogeneity. A Weibull distribution of these parameters is imposed, in such a way as to include a size effect factor in the distribution function. The well-known size effect on the failure of materials must be physically represented in any statistical failure model not only for the representations of bodies in the simulation (e.g., an armor plate), but also for the computational elements, to mitigate element resolution sensitivity of the computations.The statistical failure model was tested in simulations of a Behind Armor Debris (BAD) experiment, and found to do a much better job at predicting the size distribution of fragments than the conventional (homogeneous) failure model. The approach used here to include a size effect in the model proved to be insufficient, and including correlated statistics and/or flaw interactions may improve the model.
Available Online:
http://www.mech.utah.edu/~brannon/pubs/7-2011MeyerBrannon_IE_1915_final_onlinePublishedVersion.pdf
http://www.sciencedirect.com/science/article/pii/S0734743X10001466
R.M. Brannon, J.M. Wells, and O.E. Strack
Realistic-looking, uneven damage zones in Brazilian simulations compare favorably with laboratory data for observable damage
Validating simulated predictions of internal damage within armor ceramics is preferable to simply assessing a models ability to predict penetration depth, especially if one hopes to perform subsequent ‘‘second strike’’ analyses. We present the results of a study in which crack networks are seeded by using a statistically perturbed strength, the median of which is inherited from a deterministic ‘‘smeared damage’’ model, with adjustments to reflect experimentally established size effects. This minor alteration of an otherwise conventional damage model noticeably mitigates mesh dependencies and, at virtually no computational cost, produces far more realistic cracking patterns that are well suited for validation against X-ray computed tomography (XCT) images of internal damage patterns. For Brazilian, spall, and indentation tests, simulations share qualitative features with externally visible damage. However, the need for more stringent quantitative validation, software quality testing, and subsurface XCT validation, is emphasized.
Swan, S. and R. Brannon (2009)
Illustration of stair-stepping typical of finite sampling from a Weibull distribution
Current simulations of material deformation are a balance between computational effort and accuracy of the simulation. To increase the accuracy of the simulated material response, the simulation becomes more computationally intensive with finer meshes and shorter timesteps, increasing the time and resource requirements needed to perform the simulation. One method for improving predictions of brittle failure while minimizing computational overhead is to implement statistical variability for the material properties being simulated. This method has low computational overhead and requires a relatively small increase in resource requirements while significantly increasing the precision of simulation results. Currently, most simulation frameworks inaccurately describe brittle and heterogeneous materials as uniform bodies of equal strength and consistency. This over-simplification underscores the need to implement statistical variability to help better predict material response and failure modes for materials that contain intermittent abnormalities such as changes in hardness, strength, and grain size throughout the specimen. Uintah, the computational framework developed by the University of Utah’s C-SAFE program, has a simplistic native Gaussian distribution function that was hard-coded into select material models. The goal of this research is to create an easily duplicable method for enabling dynamic global variability according to a Weibull distribution in constitutive models in Uintah and to implement said ability into the constitutive model Kayenta. The main application of Kayenta is to simulate geological response to penetration and perforation. For the purpose of simulating failure in brittle geological samples, the Weibull distribution produces realistic statistical scatter in constituent properties that correlates well to flaws and irregularities observed in laboratory tests.
Available online:
http://www.mech.utah.edu/~brannon/pubs/2009SWAN_spring2009UROPfinalReport.pdf
R.B. Leavy; R.M. Brannon; O.E. Strack
Weibull modulus effect on radial cracking in boron carbide simulations impacted at 400 m/s.
Sphere impact experiments are used to calibrate and validate ceramic models that include statistical variability and/or scale effects in strength and toughness parameters. These dynamic experiments supplement traditional characterization experiments such as tension, triaxial compression, Brazilian, and plate impact, which are commonly used for ceramic model calibration.The fractured ceramic specimens are analyzed using sectioning, X-ray computed tomography, microscopy, and other techniques. These experimental observations indicate that a predictive material model must incorporate a standard deviation in strength that varies with the nature of the loading. Methods of using the spherical indentation data to calibrate a statistical damage model are presented in which it is assumed that variability in strength is tied to microscale stress concentrations associated with microscale heterogeneity.
Available Online:
http://www.mech.utah.edu/~brannon/pubs/7-2009-LeavyBrannonStrack-IJACT.pdf
http://dx.doi.org/10.1111/j.1744-7402.2010.02487.x
University of Utah CSM Group 