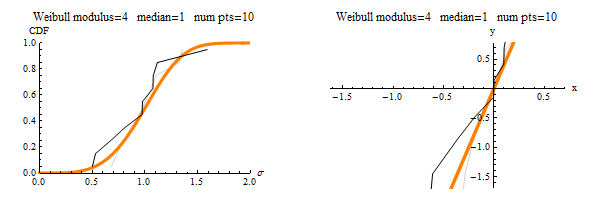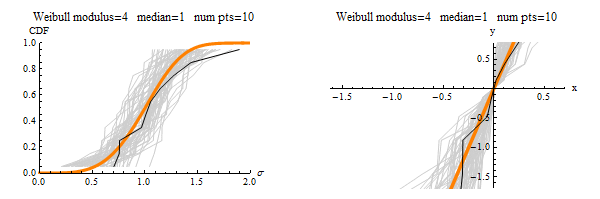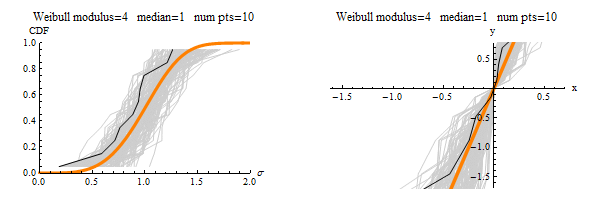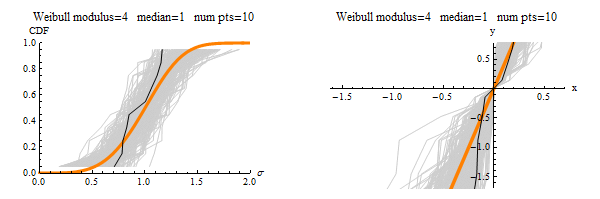Category Archives: Tutorials
Tutorials for undergraduate and graduate students and for the general public.
PowerPoint slides for Mohr’s circle
The link below provides a collection of slides used to explain Mohr’s circle in an undergraduate mechanics course at the University of Utah. If you use a Mac, it is unlikely that these will render properly (so go sit at a PC in your university computer lab to look at them). Make sure to use slideshow mode, as these have many animations!
MohrCircleFiles (zip file contains two PPT lectures and one Mathematica file)
F-tables for prescribed deformation
Motion without superimposed rotation
Same deformation with superimposed rotation
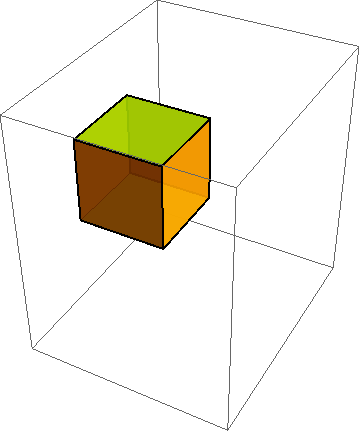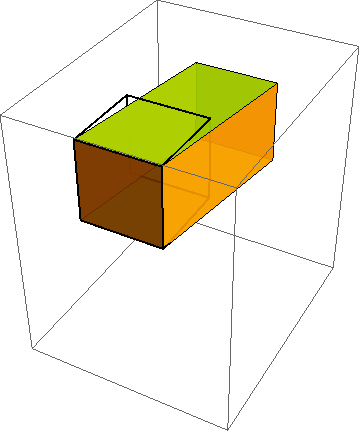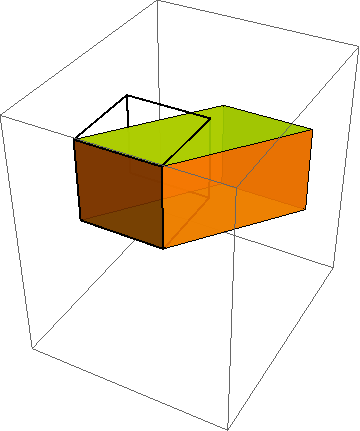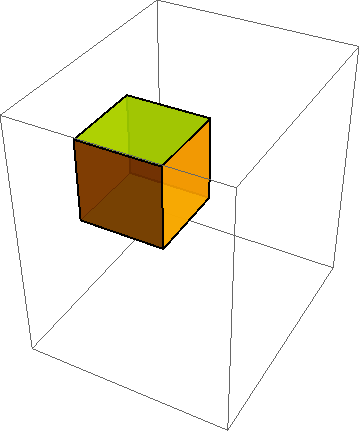
When developing constitutive models, it is crucial to run the model under a variety of standard (and some nonstandard) homogeneous deformations. To do this, you must first describe the motion mathematically. As indicated in http://csm.mech.utah.edu/content/wp-content/uploads/2011/03/GoBagDeformation.pdf, a good way to do that is to give the deformation gradient tensor, F. The component matrix [F] contains the deformed edge vectors of an initially unit cube, making this a very easy to way to prescribe deformations.
Hyphenation in technical (or other) writing.
Should you say “finite element” or “finite-element?” Which is better: a “beautifully-written” manuscript, or “beautifully written” one? Are your equations non-linear or nonlinear? Our one-page list of hyphenation rules summarizes information found in a variety of authoritative sources (Princeton Review, Strunk & White, etc.). Happy technical writing!
Making a movie for a selected part of a simulation in Visit
Here is a brief tutorial on making a movie in visit for selected portion of your simulation domain. I used sphere to represent the particles, but you do not have any restrictipn on how to show your particles. click visit_movie for the tutorial.
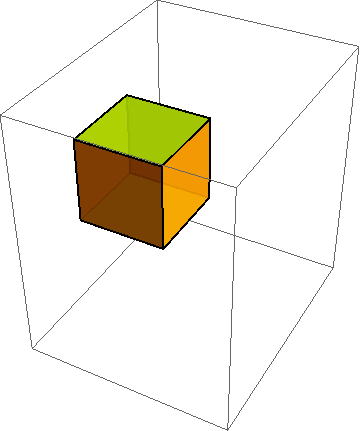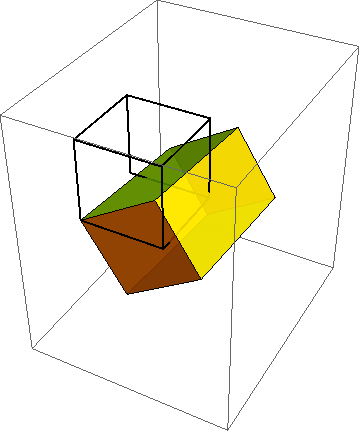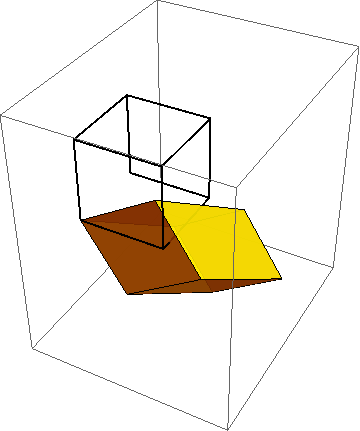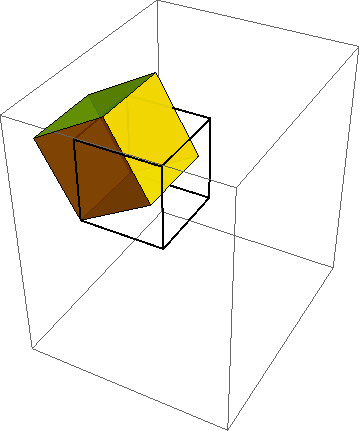
Tangent mapping
These images show the initial configuration of a body (square) and a nonlinear deformation of that body into a curvy shape (to the right of the square). Overlaid on the actual deformed shape is the so-called tangent mapping at the indicated point. It coincides with the nonlinear mapping to first-order accuracy.
Illustration of polar decomposition
This posting explains the meaning of a polar decomposition, and it gives two numerical methods for computing it.
Below is shown simple shear of a unit square. The inscribed circle and the lines from corner to corner should be regarded as painted on the material, so they flow with deformation. The green and red dashed lines show the principal directions of stretch, which are aligned with the major axes of the deformed ellipse and hence move relative to the material as the deformation proceeds. In the deformed state (far right), the red and green dashed lines are defined to be aligned with the major axes of the deformed ellipse (far right). The red and green dashed lines in the other states show the material points covered by those green and red lines in the deformed state.
Stretch, rotation, and intuition about strain rate approximations
The animation below shows
RED: simple shear in physical configuration
BLUE: simple shear with the polar rotation removed (i.e., the pure stretch)
GREEN: the deformation corresponding to the approximation that D-bar (given by the unrotated symmetric part of the velocity gradient) is actually the rate of reference logarithmic strain. This is found by integrating D-bar through time to obtain the apparent logarithmic strain, and then exponentiating this apparent strain to obtain an apparent reference stretch.
GRAY: rotation of the green deformation back to the spatial configuration.
Distinction between uniaxial stress and uniaxial strain
Uniaxial stress is a form of loading in which the 11 (axial) component of stress is nonzero, while all other components of stress are zero.
Uniaxial strain is a form of loading in which the 11 (axial) component of strain is nonzero, while all other components of strain are zero.
Math notes for entry-level grad students
This post points to a handwritten one-page summary of mathematics, at a level expected of first-year grad students specializing in engineering mechanics: http://csm.mech.utah.edu/content/wp-content/uploads/2012/05/NotesMath.jpg
University of Utah CSM Group 